RSA2048の「100万量子ビット未満での解読」報道について
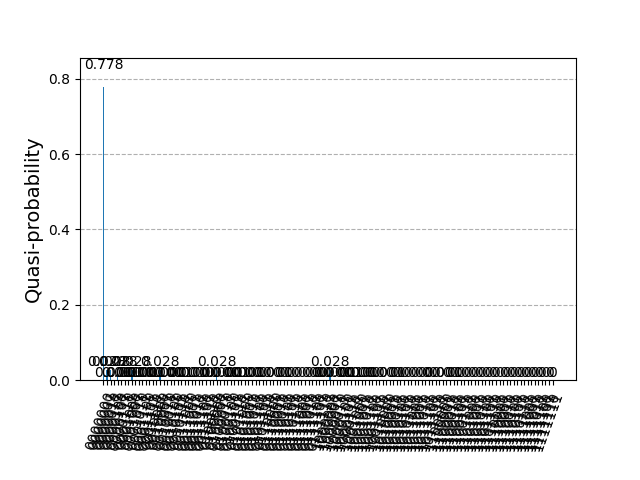
先日、「RSA 2048ビットの解読に必要な量子ビット数が100万未満となり、約1週間での解読が可能になった」という報道を目にしました。 この背景には、modの近似処理が触れられており、おそらく量子フーリエ変換(QFT)の近似にも成功していると考えられます。
複雑度の最適化:O(n²) → O(n log n)へ?
従来、量子アルゴリズムにおける演算の計算量は O(n²)〜O(n³) とされていましたが、近似処理により O(n)〜O(n log n) 程度まで最適化された可能性があります。 その結果、解読に必要な量子ビット数が劇的に削減されたと考えられます。
近似が「解」ではなく「確率振幅」に作用するという前提
もちろん、近似によって求めるべき「解」そのものが変化してしまっては意味がありません。 しかし、今回のような近似処理では解自体は変わらず、変化するのは確率振幅のみ。 つまり、従来より少ない量子ビット数でも、何度も繰り返し実行することで、統計的に正解に到達する――という考え方です。
「1週間で解読」の意味するところ
「1週間での解読」とは、1回の演算に1週間かかるという意味ではなく、1週間程度繰り返し実行すれば、期待値の範囲内で正解が1回は得られるという統計的アプローチを指しています。
たとえ期待値が低くても、十分な回数をこなせば「現実的な時間内に正解が出る」――これこそが暗号にとって最大の脅威です。
高速な検証処理がこの戦略を可能にする
このアプローチが実用的である背景には、「正解候補の検証が高速に行える」ことがあります。 たとえばRSAでもECDSAでも、提示された秘密鍵から公開鍵を導出する処理は非常に高速です。 つまり、量子コンピュータが出した秘密鍵候補が正しいかどうかを即座に判定できるため、「数撃てば当たる」戦略が現実味を帯びてきます。
解かれるのは「解」ではなく、守りの論理
最終的に、問題なのは「確率振幅の揺らぎだけで暗号が破られる」という点です。 このような近似による変化は、従来の「演算時間による守り」が通用しない世界を意味します。
脱ECDSAの重要性
周期性を内包する暗号(たとえばECDSAやRSA)は、この種の量子攻撃に非常に弱い構造を持っています。 したがって、今後は非周期型・ポスト量子暗号への移行――すなわち「脱ECDSA」が極めて重要となってくるでしょう。
量子演算の近似と確率的解法の進化は、まさに暗号の根幹を揺るがすものです。 今後の動向にも引き続き注視していく必要があります。