 bitcoin
bitcoin コンセンサス候補の選択肢が失われた気がします
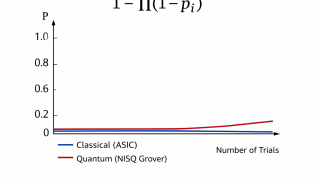
あれからコンセンサスの計算手法、調べています。でも、あらゆる計算機から検証した結果、その候補自体が失われてきた感じがします。結局、量子と人工知能が早過ぎた。それが一つの結論になるかもしれません。
 bitcoin
bitcoin  bitcoin
bitcoin  bitcoin
bitcoin  bitcoin
bitcoin  bitcoin
bitcoin  bitcoin
bitcoin  bitcoin
bitcoin  bitcoin
bitcoin  bitcoin
bitcoin  bitcoin
bitcoin  bitcoin
bitcoin  bitcoin
bitcoin 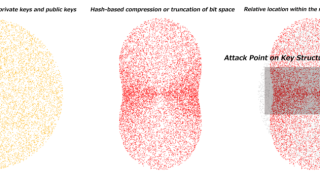 AIデータ復旧サービスについて
AIデータ復旧サービスについて  bitcoin
bitcoin  bitcoin
bitcoin